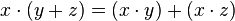Al realizar una suma podrás encontrar mayor o menor dificultad según sean las circunstancias
Ejemplo: si en una suma se debe llevar o acarrear esto hará que la dificultad se eleve un poco, pero, ¡tranquilizate! esto no sera problema si prestas atención a estos consejos.
Suma Normal
PRIMER PASO
Coloca las cantidades de una manera cuidadosa y correcta.
SEGUNDO PASO
Observa: En este tipo de sumas no se debe de realizar ningún tipo de procedimiento diferente.debido que al empezar a sumar nos damos cuenta de que los números son iguales o menores a 9(para queno sea necesario llevar al siguiente numero) y no se debe "llevar" o "acarrear"
EJEMPLO: 3+6 es igual a 9
5+2 es igual a 7
y el 4 no tiene otra cantidad, por lo tanto es igual a cuatro
TERCER PASO
Solo empieza a sumar de la manera normal empezando por el lado derecho y terminando en el izquierdo
CUARTO PASO
Da el resultado normalmente y asegurate de que este correcta
Suma "Llevando" o "Acarreando"
PRIMER PASO:
Colocación: al realizar la colocación asegúrate de tener cuidado debido que hacerlo de una manera incorrecta obtendras un resultado diferente y erróneo. asegúrate de calsar correctamente las unidades, decenas y centenas de las dos cantidades.
SEGUNDO PASO:
Inicia a sumar de izquierdaa derecha. Empezando por "3+9" luego "5+3" para terminar por "4+1" en ese orden. siempre de ixzquierda a derecha.
Cuando comienzas a sumar dte das cuenta de que 3+9 da como resultado 12 y te preguntas como colocas un 12 en una casilla? (solo se puede un numero por casilla ) que sucede entonces?
Lo que sucede es que se debe "llevar"o "acarrear". Como se hace? EL 12 es un numero compuesto por dos cifras (1 y 2)se debe separar de modo que el uno quede abajo como resultado de 3+9 y el
Observa: Otros ejemplo de lo anterior
 |
EN EL PRIMER EJEMPLO (24+7)
el 11 de 4+7 se dividió en: 1 (se queda abajo)
y el otro 1 se "llevo" junto con el 2.
EN EL SEGUNDO EJEMPLO (48+8)
el 16 de 8+8 se dividió en: 6 (se queda abajo)
y el 1 se "llevo" junto con el 4. |
 |
EN EL TERCER EJEMPLO (17+46+8)
el 21 de 7+6+8 se dividió en 1 (se queda abajo)
y el 2 que se "llevo" junto con el 1. |
TERCER PASO: Sigue sumando sin olvidarte del lunes que llevaste , este tiene que formar parte de la suma (1+5+3) lo que te dara 9
y continua asi con el (4+1) para de este modo tengas un resultado correcto.


 se lee: tres dividido cuatro.
se lee: tres dividido cuatro. .
.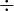 ) (también llamado "signo de la división"). Este símbolo también se usa para representar la operación de división en sí, como es de uso frecuente en las calculadoras.
) (también llamado "signo de la división"). Este símbolo también se usa para representar la operación de división en sí, como es de uso frecuente en las calculadoras. ;
; ;
; ;
; ;
; .
.