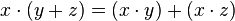Aprenda con nosotros hoy: septiembre 2013

jueves, 19 de septiembre de 2013

domingo, 15 de septiembre de 2013

Es una operación matemática que consiste en sumar un número tantas veces como indica otro número. Así, 4×3 (léase «cuatro multiplicado por tres» o, simplemente, «cuatro por tres») es igual a sumar tres veces el valor 4 por sí mismo (4+4+4).

Es una operación diferente de la suma, pero equivalente; porque permiten alcanzar el mismo resultado. La multiplicación está asociada al concepto de área geométrica.

La multiplicación se indica con un aspa (×) o el punto medio (·). En ausencia de estos caracteres se suele emplear el asterisco (*),sobre todo en computación , pero está desaconsejado en otros ámbitos y sólo debe utilizarse cuando no hay otra alternativa. A veces se utiliza la letra equis (x), pero esto es desaconsejable porque crea una confusión innecesaria con la letra que normalmente se asigna a una incógnita en una ecuación

Origen de la Multiplicación

Los primeros en usar la multiplicación fueron los egipcios, aproximadamente en el año 2700 A.C. Usaron un sistema que llamaron multiplicación por duplicación. Otra civilización pionera en usar la multiplicación fue la sumeria, en Asia menor, hacia el 2600 A.C. Inventaron las tablas de multiplicar y las escribían en tablas de arcilla secadas al sol.
La multiplicación que se usa en la actualidad, fue inventada por los hindúes.
Los chinos multiplicaban con varillas de bambú que se disponen en forma horizontal, las que corresponden al multiplicando y en forma vertical las que corresponden al multiplicador.

Pitágoras: filósofo griego, fue el llamado desarrollador y analizador de la multiplicación.

Relevancia en vida cotidiana, es habitual porque se hace sin darse cuenta.Es como la suma, pero nos ayuda a simplificarla y se nos a hace mas fácil obtener resultados.Sirve para distribuir y saber cuánto se necesita de ciertos recursos

Ejemplo•Si medio kilo de pan cuesta 400 colones,para saber el precio del kilo del pan podemos multiplicar 400 por 2, lo que dará 800 colones.

PARTES DE LA MULPLICACION

NOTACION

PROPIEDADES DE LA MULTIPLICACION

Para los números naturales, enteros, fracciones y números reales y complejos, la multiplicación tiene ciertas propiedades:

Propiedad conmutativa
El orden de los factores no altera el producto.

$x\cdot y = y\cdot x$

Propiedad asociativa

Únicamente expresiones de multiplicación o adición son invariantes con respecto al orden de las operaciones.

$(x\cdot y)\cdot z = x\cdot(y\cdot z)$

Propiedad distributiva

El total de la suma de dos números multiplicado por un tercer número es igual a la suma de los productos entre el tercer número y cada sumando.

$x\cdot(y + z) = (x\cdot y) + (x\cdot z)$

Elemento identidad (neutro)

La identidad multiplicativa es 1; el producto de todo número multiplicado por 1 es sí mismo. Esto se conoce como la propiedad de identidad.

$x\cdot 1 = x$

Elemento cero (absorbente)

Cualquier número multiplicado por cero da como producto cero. Esto se conoce como la propiedad cero de la multiplicación.

$x\cdot 0 = 0$

$0\cdot x = 0$

LAS TABLAS DE MULPLICAR

sábado, 7 de septiembre de 2013

Video de apoyo

Aqui les dejo un excelente video que les podra ayudar a comprender mas fácil mente el tema de la resta y la suma

La resta

La resta o sustracción es una de las cuatro operaciones básicas de la aritmética; se trata de una operación de descomposición que consiste en, dada cierta cantidad, eliminar una parte de ella, y el resultado se conoce como diferencia o resto.Es la operación inversa a la suma. Por ejemplo, si a+b = c, entonces c–b = a.

En la resta, el primer número se denomina minuendo y el segundo es el sustraendo. El resultado de la resta se denomina diferencia.

En el conjunto de los números naturales, N, sólo se pueden restar dos números si el minuendo es mayor que el sustraendo. De lo contrario, la diferencia sería un número negativo, que por definición estaría excluido del conjunto. Esto implica la ampliación del conjunto de los números naturales con un nuevo concepto de número, el conjunto de los números enteros Z, que incluye a los naturales. Esto también es así para otros conjuntos con ciertas restricciones, como los números reales positivos.

El procedimiento estándar de una resta

Se procede colocando el minuendo encima del sustraendo, ordenando las cifras en columnas de derecha a izquierda según el orden de unidades, decenas, centenas etc. igual que en la suma.

A continuación se comienza restando la cifra de la columna de unidades del minuendo al sustraendo, teniendo en cuenta que si la cifra del minuendo es menor que la del sustraendo se suma a la cifra 10 unidades, colocando en la línea de acarreo sobre la columna siguiente (las decenas) un 1, que se sumará a la cifra del sustraendo de las decenas. Una vez hecho esto se restan las cifras de minuendo a sustraendo de la columna unidades y se escribe la cifra resultado en la línea de resto de la misma columna. De igual manera, se procede en la columna de las decenas, centenas, unidades de millar, etc. sin olvidar sumar los acarreos de columnas anteriores al sustraendo debido a la suma de diez unidades en la columna anterior a la cifra del minuendo si éste es menor que el sustraendo.

La cifra 0 en el minuendo se considera como un 10, mientras que en el sustraendo no tiene ningún efecto.

Como ejemplo ilustrativo del proceso de restado de dos números, se utilizarán el 1419 y 751, obteniéndose:

$\begin{array}{rrrrr} & \color{Red}1 & \color{Red}1 & & \\ & M & C & D & U \\ & 1 & 4 & 1 & 9 \\ & & 7 & 5 & 1 \\ \hline & 0 & 6 & 6 & 8 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow \rm acarreo }\\ \\ \longleftarrow \; \rm Minuendo\\ \longleftarrow \; \rm Sustraendo\\ \longleftarrow \rm{Resto \; o \; Diferencia}\\ \end{array}$

La comprobación del resultado como «Resto o Diferencia» se hace sumando dicho resultado con el sustraendo, ya que en toda resta se cumple que: Sustraendo + Diferencia = Minuendo, o sea, el resultado de dicha suma debe de ser el minuendo, en este caso ejemplo sería 668+751=1419.

La suma

La suma o adición es una operación básica por su naturalidad, que se representa con el signo (+), el cual se combina con facilidad matemática de composición en la que consiste en combinar o añadir dos números o más para obtener una cantidad final o total. Por otro lado, la acción repetitiva de sumar uno es la forma más básica de contar.

Propiedades de la suma

Propiedad conmutativa:

Si el orden de los factores cambia no altera el resultado:

a+b=b+a.

Propiedad asociativa:

Propiedad que establece que cuando se suma tres o más números, la suma siempre es la misma independientemente de su agrupamiento.

Un ejemplo es: a+(b+c) = (a+b)+c.

Elemento neutro:

0.Para cualquier número a, a + 0 = 0 + a = a.

Elemento opuesto o inverso aditivo:

Para cualquier número entero, racional, real o complejo a, existe un número −a tal que a + (−a) = (−a) + a = 0. Este número −a se denomina elemento opuesto, y es único para cada a. No existe en algunos conjuntos, como el de los números naturales.

Propiedad distributiva:

La suma de dos números multiplicada por un tercer número es igual a la suma del producto de cada sumando multiplicado por el tercer número. Por ejemplo, (6+3) * 4 = 6*4 + 3*4.

Propiedad de cerradura:

Cuando se suman números naturales el resultado es siempre un número natural. Por ejemplo a+b=c.

El procedimiento estándar de una suma

El procedimiento estándar para efectuar sumas de varios números, llamados "sumando", es el siguiente:

Los sumandos se colocan en filas sucesivas ordenando las cifras en columnas, empezando por la derecha con la cifra de las unidades(U), a la izquierda las decenas(D), la siguiente las centenas(C), la siguiente los millares(M), etc.

La suma de los números 750 + 1583 + 69 se ordenarían de la siguiente forma:

$\begin{array}{rrrrr} & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline \end{array} \begin{array}{l} \\ \longleftarrow 1^{\circ} \; \textrm{sumando}\\ \longleftarrow 2^{\circ} \; \textrm{sumando}\\ \longleftarrow 3^{\circ} \; \textrm{sumando}\\ \end{array}$

Se suman en primer lugar las cifras de la columna de las unidades según las tablas elementales, colocando en el resultado la cifra de unidades que resulte; cuando estas unidades sean más de 10 las decenas se acumulan como un sumando más en la fila de acarreo.

En este caso 3 más 9 son 12, el 2 del 12 se pone en la parte inferior y el 1 se pasa como acarreo en la columna siguiente.

$\begin{array}{rrrrr} & & & 1 & \\ & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline & & & & 2 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow \textrm{acarreo} }\\ \\ \longleftarrow 1^{\circ} \; \textrm{sumando}\\ \longleftarrow 2^{\circ} \; \textrm{sumando}\\ \longleftarrow 3^{\circ} \; \textrm{sumando}\\ \\ \end{array}$

En la columna de las decenas, procediendo entonces a la suma de esa columna como si fueran unidades.

Sumamos el 1 del acarreo más 5, 8 y 6 que dan un total de 20, el 0 de 20 se pone en la parte inferior como resultado y el 2 se pasa como acarreo a la columna siguiente.

$\begin{array}{rrrrr} & & 2 & 1 & \\ & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline & & & 0 & 2 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow \textrm{acarreo} }\\ \\ \longleftarrow 1^{\circ} \; \textrm{sumando}\\ \longleftarrow 2^{\circ} \; \textrm{sumando}\\ \longleftarrow 3^{\circ} \; \textrm{sumando}\\ \\ \end{array}$

Se procede de igual forma con la columna de las decenas, acarreo incluido, colocando en la fila de acarreo sobre la columna de las centenas las decenas (de unidades de decenas).

En la columna de las centenas tenemos, el 2 de acarreo, el 7 y el 5 que sumados dan 14, el 4 del 14 se pone en la parte inferior y el 1 se pasa a la siguiente columna como acarreo.

$\begin{array}{rrrrr} & 1 & 2 & 1 & \\ & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline & & 4 & 0 & 2 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow \textrm{acarreo} }\\ \\ \longleftarrow 1^{\circ} \; \textrm{sumando}\\ \longleftarrow 2^{\circ} \; \textrm{sumando}\\ \longleftarrow 3^{\circ} \; \textrm{sumando}\\ \\ \end{array}$

Se procede de igual forma con todas las columnas, añadiendo a la columna última de la izquierda las decenas de la columna anterior en vez de subir a la fila de acarreo.

En la columna de los millares tenemos 1 de acareo más el 1 de sumando que sumados dan 2, que se pone en la parte inferior como resultado, al no haber más sumandos damos por finalizada la operación.

$\begin{array}{rrrrr} & 1 & 2 & 1 & \\ & M & C & D & U \\ & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline & 2 & 4 & 0 & 2 \\ \end{array} \begin{array}{l} { \color{Red}\longleftarrow \textrm{acarreo} }\\ \\ \longleftarrow 1^{\circ} \; \textrm{sumando}\\ \longleftarrow 2^{\circ} \; \textrm{sumando}\\ \longleftarrow 3^{\circ} \; \textrm{sumando}\\ \longleftarrow \textrm{total}\\ \end{array}$

Normalmente los acarreos o llevadas no se anotan en el papel, sumando directamente el acarreo a los sumandos de la columna siguiente y el aspecto de la realización de la suma sin las anotaciones auxiliares sería el siguiente:

$\begin{array}{rrrrr} & & 7 & 5 & 0 \\ & 1 & 5 & 8 & 3 \\ + & & & 6 & 9 \\ \hline & 2 & 4 & 0 & 2 \\ \end{array}$

Operaciones Matematicas Basicas

¿Que es una operacion matematica?

Una operacion matematica es la relacion de dos conjuntos o cifras que según sea el criterio de la operacion sea una suma, o una resta o divicion se llega a un resultado.

10+5=15

10-5=5

10*5=50

10÷5=2

En este ejemplo observamos que apesar de que las dos cifras (10 y 5) sean las misma en todos las operaciones, el signo propuesto permite que el resultado obtenido sea totalmente diferente. Eso nos afirma que las operaciones matematicas tienen sus propias caracteristicas y utilidades

Las 7 operaciones básicas de la Aritmética son:

Suma o adición

Resta o sustracción

Multiplicación o producto

División o cociente

Potenciación

Logaritmación

Operaciones Matemáticas en la antiguedad

Los antiguos operaban con números naturales y fracciones unitarias, basando su aritmética en el principio aditivo, la capacidad de multiplicar y dividir por dos y la capacidad de hallar los dos tercios de cualquier número.

En el papiro de Ahmes o Rhin las operaciones de sumar y restar aparecen representadas por un dibujo esquemático de las piernas de una persona que se acerca y que se aleja.
Para sumar y restar se limitaban a combinar y cancelar los diferentes símbolos, hasta llegar al resultado:
364 + 752 = 1.116

¿Para que servían la operaciones matemáticas en la antigüedad?

Eran utilizadas, de una manera indirecta y sin saberlo, diariamente en sus actividades, por ejemplo para elaborar un "inventario" de las cosechas, contar sus animales, llevar cuentas de los dias, conocer la cantidad de sus pertenencias entre otras cosas. De esa manera las operaciones basicas y la matematica en general inicio un largo proceso hasta terminar siendo esencial en la vida de cada uno de nosotros

Las operaciones matematicas en la actualidad

Los programas de educacion en las escuelas y colegios de todos los paises incluyen las operaciones matematicas como un tema basico e indispensable que no pueden faltar y aumenta de dificultad con respecto al grado que se curse. los niños desde sus primeros años escolares se le enseña por medio de juegos, practicas e ilustraciones a sumar, restar, multiplicar y dividir. Al ser las operaciones matematicos un tema desconocido en esas edades tiende a ser dificultoso para algunos pequeños por lo que el programa recomienda que se trate con cuidado y mucha paciencia, ademas de usar la creatividad y tecnicas nuevas para enseñarlo